Burt.K
Awesome Discovery
모나드와 함수형 아키텍처 3장. 모나드
Table of Contents
3장. 모나드
$$ a \circ b \circ c \circ … \circ x \circ y \circ z $$
함수 합성식입니다. 모나드뿐 아니라 함수형 프로그래밍의 본질이 모두 담겨 있는 식입니다. 사실 모든 이야기는 여기서부터 시작됩니다. 수학에서 이렇게 함수를 합성할 수 있는 이유는 수학의 함수가 순수 함수이기 때문입니다. 1부. 시작하기에서 함수는 두 집합을 연결하여 관계를 만들어 주는 연산으로 정의했습니다. 두 집합을 연결할 때 닫힘과 열림이라는 중요한 얘기를 해야 합니다.
3-1. 닫힘과 열림
집합 $A$에 대하여 이항연산을 수행할 때 연산 결과가 같은 집합 $A$의 원소이면 해당 이항연산은 집합 $A$에 닫혀 있다고 합니다. 자연수 집합 $N$에서 $+$연산은 자연수 집합에 닫혀 있습니다.
$$ 1 + 2 = 3 $$
집합 $A$에 대하여 이항연산을 수행할 때 연산 결과가 같은 집합 $A$의 원소가 아니면 해당 이항연산은 집합 $A$에 열려 있다고 합니다. 자연수 집합 $N$에서 $-$연산은 자연수 집합에 열려 있습니다.
$$ 1 - 1 = 0 $$
$0$은 자연수 집합에 포함되어 있지 않기 때문에 자연수 집합 $N$에서 $-$ 연산은 열려 있습니다. 열려 있는 경우에는 우리가 알고 있는 집합이 확장되는 것으로 볼 수 있습니다. 연산 결과로 연결되어야 할 집합을 찾게 된 것입니다. 이 예제에서 우리는 $0$을 포함하고 있는 정수 집합 $Z$를 찾게 된 것입니다. 한 번 더 예를 들어보겠습니다. 정수 집합 $Z$는 $\times$ 연산에 대해 닫혀 있습니다.
$$ -1 \times -2 = 2 $$
하지만 $\div$ 연산은 열려 있습니다.
$$ 1 \div 10 = 0.1 $$
정수 집합은 나눗셈 연산에 열려 있으며 0.1이 포함된 새로운 집합을 찾아야 합니다. 유리수 집합 $Q$를 찾게 됩니다. 이제 우리가 알고 있는 수의 집합은 자연수에서 유리수까지 확장되었습니다. 이를 정리하면 아래와 같습니다.
$$ A: N \rightarrow N $$
$$ f: N \rightarrow Z $$
$$ B: Z \rightarrow Z $$
$$ g: Z \rightarrow Q $$
$$ C: Q \rightarrow Q $$
위 정리에서 $f$는 $-$ 연산에 해당하고 $g$는 $\div$ 연산에 해당합니다. 이것을 보고 사람들은 $f$와 $g$를 합성할 수 있지 않을까? 생각했습니다.
$$ g \circ f: N \rightarrow Q $$
이를 그림으로 표현하면 아래와 같습니다.
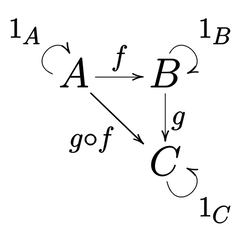
이 그림은 카테고리 이론(이하 범주론)을 설명하는 그림입니다. 그림에서 $A$, $B$, $C$ 를 연결하는 화살표에서 $f: A \rightarrow B$ 가 있고 $g: B \rightarrow C$ 가 존재하면 반드시 $g \circ f: A \rightarrow C$ 가 존재한다는 것이 카테고리 이론입니다. 카테고리 이론은 수학의 여러 분야에서 공통으로 발생하는 현상들을 추상화를 통해 정리한 분야입니다. 함수 합성을 중심으로 추상화를 합니다. 카테고리 이론으로 컴퓨터 프로그램을 추상화하면 함수의 합성으로 추상화할 수 있습니다. 컴퓨터 프로그램의 모든 것을 함수의 합성으로 표현하기 위해서 카테고리, 펑터, 모노이드, 모나드 등을 사용합니다.
카테고리 이론에서 $g \circ f: A \rightarrow C$ 가 중요한 내용입니다. 이 정리가 있어서 함수 합성은 빅뱅처럼 폭발적으로 확장됩니다. 시간이 지날수록 컴퓨터 프로그램에 신규 기능을 추가하면 프로그램의 덩치가 커지는데 함수 합성을 적용하면 큰 문제 없이 확장할 수 있습니다.
$$ p: g \circ f $$
$$ k: q \circ p $$
$$ … $$
거꾸로 생각하면 덩치가 큰 문제를 작은 문제로 나누어 풀 수 있다는 것을 의미합니다. 텍스트 파일을 열어 모든 문자를 대문자로 변경한 후 화면에 출력하는 문제를 생각해 봅시다. 이 문제를 함수로 잘게 나누어 표현해 보면 아래와 같습니다.
$$ p: 텍스트 파일 \rightarrow 텍스트 문자열 $$
$$ q: 텍스트 문자열 \rightarrow 대문자 텍스트 문자열 $$
$$ r: 대문자 텍스트 문자열 \rightarrow 대문자 텍스트 문자열 화면에 출력 $$
이 것을 카테고리 이론으로 표현해 보면 아래와 같습니다.
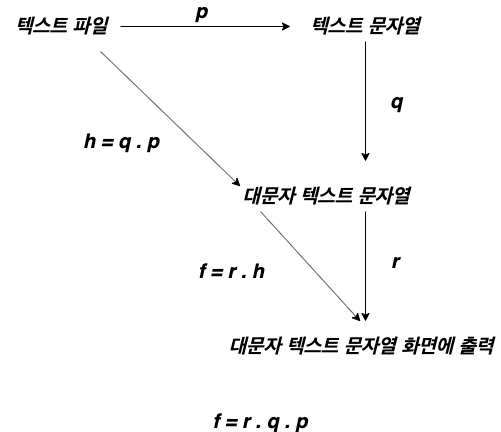
$$ f: 텍스트 파일 \rightarrow 대문자 텍스트 문자열 화면에 출력 $$
위처럼 작동하는 함수를 잘게 나누어 해결하고 각 결과를 합성하여 결국 원하는 함수를 만들 수 있음을 알 수 있습니다.
$$ f: r \circ q \circ p $$
카테고리 이론에 대한 정말 좋은 책이 있습니다. Category Theory for Programmers 책으로 온라인으로 무료로 제공되고 있습니다. 카테고리 이론에 관한 내용은 이 책을 참고하시면 좋을 것 같습니다.
3-2. 순수 함수와 사이드 이펙트
1부에서 사이드이펙트를 알아보았습니다. 사이드이펙트가 발생하는 위치에 따라 나누어 보면, 함수 외부와 내부에서 발생하는 사이드이펙트로 나눌 수 있습니다. 만약 독립된 함수로 외부에 영향을 주지도 받지도 않는 함수가 존재한다고 생각해 봅시다. 이 함수는 파일 이름을 받아 파일을 반환해야 하는 함수라면 어떨까요?
$$ f: FileName \rightarrow FILE $$
내부에서도 사이드이펙트가 발생하지 않고 항상 $FILE$을 반환한다면 함수 $f$는 순수함수가 될 것입니다. 하지만 $FileName$해당하는 파일이 없을 수도 있습니다. 이럴 때는 무엇을 반환해야 할까요? 포인터를 자주 사용하는 C언어에서는 이중 포인터를 사용하여 오류 발생 시 결과 이외의 오류 값을 담을 수 있는 Error 변수의 이중포인터를 함수 인자로 같이 넘겨 주곤 했습니다. C++, Java 같은 언어는 Exception을 도입하여 결과 이외의 값을 예외로 처리하도록 했습니다. 두 방법 모두 순수함수 성질을 깨는 것입니다. 순수 함수성이 깨지는 것을 조심해야 하는 이유는 함수 합성을 더 이상 할 수 없기 때문입니다. 즉, 독립된 함수일 때 결과값 집합 이외의 집합값을 반환할 때 사이드이펙트가 있다고 얘기할 수 있습니다.
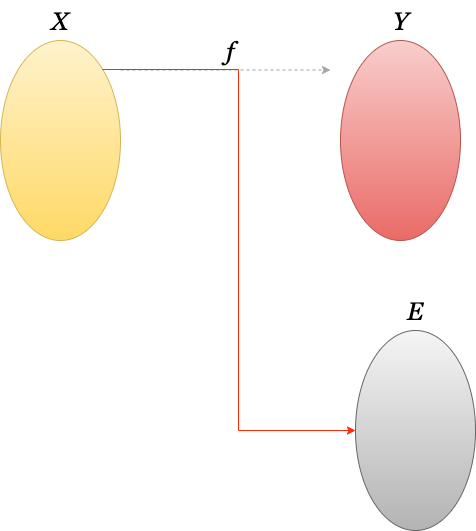
3-3. 모나드란 무엇인가?
그렇다면 이렇게 생각해 볼 수 있습니다. 결과값 집합과 오류값 집합을 하나의 집합으로 만들면 어떨까? 라고 말입니다.
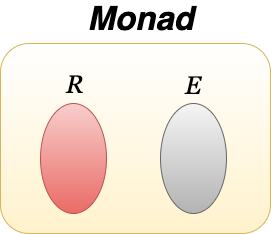
지금까지 말하고 싶었던 모나드는 함수 내부에서 발생할 수 있는 사이드이펙트를 결과 집합과 함께 포함하는 타입입니다. 함수 실행 결과를 항상 모나드로 반환하여 순수함수 성질을 잃지 않게 하는 것입니다. 더 정확하게 얘기하자면 원시타입(boolean, int, string, float, double)과 커스텀 타입(class, struct)을 구체타입이라고 할 때 우리는 구체타입을 사용하여 함수의 인자와 결과값을 표현했습니다. 이 구체타입을 한 번 더 추상화한 것이 모나드입니다.
$$ f: FileName \rightarrow Monad[FILE, Error] $$
노트 이후로 { 원시타입, enum, struct, class } 를 모나드와 비교해 구체타입으로 칭하겠습니다.
함수의 결과값에 모나드를 적용하면 내부에서 어떤 사이드이펙트가 발생하던 그 함수 자체는 순수 함수로 만들 수 있습니다. 이를 좀 더 응용하면 사이드이펙트가 아닌 다른 집합을 포함하는 타입을 생각할 수 있습니다. 자주 쓰는 모나드 중 $Either$가 대표적인 예입니다. $Either$모나드는 $Left$와 $Right$를 가지고 있는 타입으로 $Either[Left, Right]$라고 정의할 수 있습니다. $Either$에 대한 내용은 잠시 뒤에 다시 살펴보겠습니다.
모나드는 함수에 들어가고 반환되는 값을 한차례 추상화한 것입니다. $f: int \rightarrow int$ 함수가 있을 때, 함수 인자 또는 반환값을 추상화하는 것이죠. C++나 Java를 배울 때, 원시타입인 int, string, double, boolean 등을 모아 class를 통해 추상화하듯이 말이죠. 추상화는 한번 감싸는 것으로 생각할 수 있습니다. 그 과정에서 개발자는 어떤 의미를 심을 수 있습니다. C++에서 원시타입과 메서드를 모아 Person으로 추상화하듯이 말입니다. Maybe 모나드는 값이 있거나 없거나라는 의미를 담습니다. 이것이 모나드의 강력한 힘입니다. 구체타입을 추상화하면서 의미를 동시에 담을 수 있게 되어 마치 사람이 생각하는 것처럼 함수를 작성할 수 있습니다.
함수의 사이드이펙트를 포함하여 함수의 인자나 결과값을 추상화하는 모나드를 살펴보았습니다. 하지만 이것은 구조체나 클래스로도 정의 가능합니다. 하지만 모나드를 더욱 구분지어주는 특징이 하나 더 있습니다. 바로 합성을 통해 흐름을 만드는 것입니다. 흐름을 만들기 위해서 특별히 해주는 일이 있습니다. 어떤 것인지 살펴봅시다.
3-4. 합성, 흐름 그리고 빅뱅
우리는 거인의 어깨 위에 앉아 있습니다. 구조적 프로그래밍 그리고 객제지향 프로그래밍이 쌓아온 수많은 함수와 타입 위에 앉아 있는 것이지요. 모나드를 통해 함수를 합성하기 위해서는 함수의 인자와 결과값이 모두 모나드로 되어 있어야 합니다.
$$ f: Monad \rightarrow Monad $$
$$ g: Monad \rightarrow Monad $$
$$ h: Monad \rightarrow Monad $$
$$ h \circ g \circ f: Monad \rightarrow Monad \rightarrow Monad $$
간단한 Monad를 정의해 보겠습니다. Result<T>이란 모나드로 [Success, Fail] 집합을 포함합니다. 함수에서 내부 연산 중 사이드이펙트가 발생하면 Fail을 반환합니다.
sealed class Result<T> {
data class Success<T>(val value: T): Result<T>()
class Fail<T>: Result<T>()
}Result
구체타입만을 쓰는 함수는 아래와 같을 것입니다.
fun div(a: Int, b: Int): Int {
return a / b
}여러분도 잘 알듯이 이 함수는 사이드이펙트를 가지고 있습니다. 만약 b가 0일 경우 java.lang.ArithmeticException: / by zero라는 예외가 발생합니다. 이 예외를 처리해 보겠습니다.
fun div(a: Int, b: Int): Int {
try {
return a / b
} catch (e: Throwable){
return -1
}
}만약 위처럼 작성했다면 문제는 해결할 수 있지만 결과값이 모호해집니다. div(a, -a) 또는 div(-a, a) 때의 결과값과 예외가 발생했을 때 반환하는 -1을 구분할 수 없기 때문입니다.
이제 결과값을 모나드로 추상화해 보겠습니다. 위에서 정의한 Result
fun div(a: Int, b: Int): Result<Int> {
try {
return Result.Success(a / b)
} catch (e: Throwable){
return Result.Fail()
}
}실제로 사용해 봅시다.
val result1 = div(10, 2)
val result2 = div(10, 0)위 result를 사용하려면 어떻게 해야 할까요? 각 result가 Success인지 Fail인지 검사해야 합니다. 아래처럼 말입니다.
fun main(args: Array<String>) {
val result1 = div(10, 2)
val result2 = div(10, 0)
when (result1) {
is Result.Success -> { println(result1.value) }
is Result.Fail -> { println("result1 is Failed") }
}
when (result2) {
is Result.Success -> { println(result2.value) }
is Result.Fail -> { println("result2 is Failed") }
}
}아래는 출력된 결과입니다.
5
result2 is Failed모나드 Result
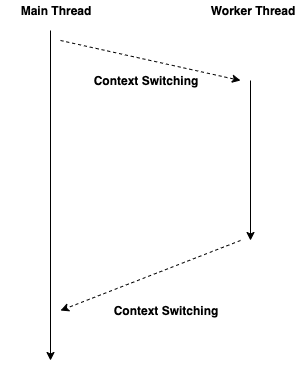
위 그림에서 워커 스레드에서 메인 스레드에 값을 바로 쓰거나 UI에 접근하거나 하면 프로그램이 오작동을 일으킬 수 있습니다. 그래서 콜백, Rx, async/await 등 그 어떤 것을 사용하더라도 컨텍스트 스위칭을 피할 수는 없습니다. 즉, 워커 스레드에서 계산한 값을 메인 스레드에서 사용하기 위해서는 어떤 번거로운 작업이 필요합니다.
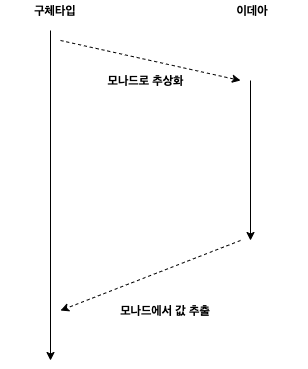
모나드를 사용한 코드가 이와 비슷하지 않나요? 마치 플라톤의 이데아 이론 같기도 합니다. 구체타입 세계와 추상화로 이뤄진 이데아가 있다고 볼 수 있습니다. 객체지향에서는 원시타입들을 class라는 도구를 사용해 추상화하였고 그것을 원시타입 세계에서 사용하기 위해서는 인스턴스를 만들어야만 했습니다. 모나드도 마찬가지입니다.
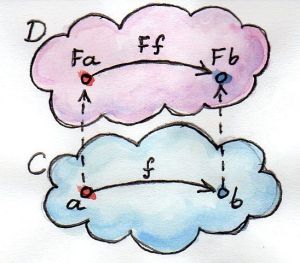
아래는 Category Theory for Programmers 책에서 Functor를 표현한 그림으로 구체타입 세계와 모나드 세계를 표현하고 있습니다.
기억할 점은 구체타입을 추상화한 모나드에서 값을 얻기 위해서는 스레딩의 컨텍스트 스위칭처럼 부가적인 작업이 필요하다는 것입니다.
위에서 만든 모나드를 통해서 함수를 합성해 봅시다. 어떤 정수를 입력하면 정수값에 10을 계속해서 곱하는 함수 합성입니다. 단, 0 이하의 값을 입력하면 Fail을 반환하고 모나드에서 값을 추출할 때 Fail이면 -1을 반환한다고 가정합니다.
fun a(value: Int): Result<Int> {
if (value > 0) {
return Result.Success(value * 10)
} else {
return Result.Fail()
}
}
fun b(value: Result<Int>): Result<Int> {
return when (value) {
is Result.Success -> {
Result.Success(value = value.value * 10)
}
is Result.Fail -> {
value
}
}
}
fun c(value: Result<Int>): Int {
return when (value) {
is Result.Success -> {
value.value
}
is Result.Fail -> {
-1
}
}
}
fun d(value: Int): Int {
return value * 10
}$$ f(10) = c \circ b \circ b \circ b \circ b \circ a(10) $$
위 함수 합성식을 코드로 나타내면 아래와 같습니다.
val result = c(b(b(b(b((a(10)))))))
println(result)
// 출력
1000000val result = c(b(b(b(b((a(-10)))))))
println(result)
// 출력
-1원하는 만큼 함수를 합성할 수 있습니다. 하지만 함수 합성식이 자연스럽지 않습니다. 코드를 이해하기가 더 어려워진 것 같습니다. 뭔가 흐르는 것처럼 표현할 수 있을까요? 멤버 함수나 연산자 재정의를 사용해 봅시다.
infix fun <T> Result<T>.compose(functor: (value: Result<T>) -> Result<T>): Result<T> {
return functor(this)
}
infix fun <T> Result<T>.compose2(functor: (value: Result<T>) -> T): T {
return functor(this)
}functor 라는 람다를 받아서 functor를 실행하여 Result
위의 compose 함수를 사용하면 아래처럼 함수 합성식을 표현할 수 있습니다.
val result1 = a(10) compose ::b compose ::b compose ::b compose ::b compose2 ::c
println(result1)
// 출력
1000000val result2 = a(-10) compose ::b compose ::b compose ::b compose ::b compose2 ::c
println(result2)
// 출력
-1뭔가가 함수 사이로 흐르는 것 같습니다. compose 연산자를 사용하면 함수 a, b, c를 끝이 없이 합성할 수 있을까요? 그렇지 않습니다. 함수 a는 구체타입 T를 받아서 모나드 Result
val result3 = a(10) compose ::b compose2 ::c compose ::a // <- 여기서 연결이 끊어집니다.만약 이를 해결하기 위해서 아래처럼 compose3를 정의한다고 생각해 봅시다.
infix fun <T> Result<T>.compose2(functor: (value: T) -> Result<T>): Result<T> {
when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
functor(어떤 값을 넣어야 하죠?)
}
}
}네 그렇습니다. this는 현재 이데아를 걷고 있는 추상화된 모나드이기 때문에 functor에 구체타입 값을 넣어주기 위해서는 자기 자신으로부터 값을 추출해야 합니다. 하지만 위의 경우 어떤 값을 넣어야 할지 기준이 없습니다. 물론 첫 가정에서 Fail 때는 -1 을 반환하면 된다고 했지만, 그 가정이 변경되거나 정해지지 않았다면 어떤 값을 넣어야 할지 정할 수가 없습니다.
그리고 우리가 정의한 함수 a, b, c의 프로토타입을 살펴봅시다.
fun a(value: Int): Result<Int>
fun b(value: Result<Int>): Result<Int>
fun c(value: Result<Int>): Int어떤가요? 우리는 보통 이런 식으로 함수를 정의하지 않습니다. 우리가 사용하는 외부 함수나 라이브러리 그리고 프레임워크의 함수들도 위처럼 정의되어 있지 않습니다. 구체타입을 인자로 받고 결과값을 반환합니다. 아래처럼 말입니다.
fun d(value: Int): Int 우리는 거인의 어깨 위에 앉아 있고 거인을 조종할 수 있어야 합니다. 즉, 거대한 라이브러리와 프레임워크의 함수들을 합성을 통해 사용할 수 있어야 합니다. 이 함수들을 감싸 안을 방법이 필요합니다.
3-5. map과 flatMap
위에서 정의한 Result
map 함수는 구체타입을 이데아로 연결해 주는 함수이며 flatMap 은 이데아를 계속 거닐게 해주는 함수입니다. flatMap의 이름에 flat이 들어가는 이유는 함수를 합성하다 보면 중첩된 Monad[Monad[V]]가 발생할 수 있기 때문에 이것을 펼쳐서 하나의 Monad[V]로 만들어 준다고 하여 flat 단어가 이름에 들어가게 되었습니다. 그렇지만 저는 map 함수는 구체타입을 이데아로 연결해 주는 함수이며 flatMap 은 이데아를 계속 거닐게 해주는 함수입니다. 라는 설명이 더욱 마음에 듭니다.
Result
infix fun <T, R> Result<T>.map(functor: (value: T) -> R): Result<R> {
return this.flatMap { value ->
Result.Success(functor(value))
}
}
infix fun <T, R> Result<T>.flatMap(functor: (value: T) -> Result<R>): Result<R> {
return when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
Result.Fail()
}
}
}map 함수가 받는 functor는 구체타입 T를 받고 결과로 구체타입 R을 반환하는 람다입니다. 즉, 이 람다는 내부의 사이드이펙트가 없는 순수함수로 가정해야 합니다. 만약 사이드이펙트가 있는 함수는 함수 a처럼 구체타입을 받고 추상화된 모나드를 반환하는 함수로 정의해야 합니다. 다시 map 함수를 보면 내부에서 flatMap을 사용해 Result 모나드로 감싸고 있습니다. Success를 사용할 수 있는 이유는 functor가 순수함수라고 정의했기 때문입니다. 즉, 반환되는 구체타입을 map을 거치면 추상화된 모나드로 연결하여 주므로 map은 구체타입을 이데아로 연결해 주는 함수입니다.
flatMap을 보면 functor는 구체타입을 받고 결과로 모나드를 반환하는 람다입니다. 즉, 사이드이펙트가 존재할 수 있는 함수만을 받을 수 있습니다. 이전에 정의했던 함수 a처럼 내부에서 사이드이펙트를 모나드로 처리하여 순수함수성을 지키는 함수만 flatMap을 사용할 수 있고 결과는 계속해서 모나드로 이어지기 때문에 flatMap을 이데아를 거닐게 하는 함수로 볼 수 있는 것입니다.
map과 flatMap을 사용하여 합성해 봅시다. 방금 알아보았듯이 함수 a, d만 이용할 수 있습니다. 함수 b는 flatMap을 사용하여 표현할 수 있기 때문에 필요가 없습니다. 함수 c는 모나드에서 값을 추출하는 것이므로 계속 필요합니다. 함수 c의 이름을 쉽게 이해하기 위해서 value로 변경하겠습니다.
fun a(value: Int): Result<Int> {
if (value > 0) {
return Result.Success(value * 10)
} else {
return Result.Fail()
}
}
fun d(value: Int): Int {
return value * 10
}
fun value(value: Result<Int>): Int {
return when (value) {
is Result.Success -> {
value.value
}
is Result.Fail -> {
-1
}
}
}합성해 보겠습니다.
val flow1 = a(10) map ::d flatMap ::a
println(value(flow1))
//출력
10000원하는 결과를 얻었습니다. value 함수가 Int뿐 아니라 다른 타입에 대해서 동작하도록 Rx처럼 값을 얻게 Result
sealed class Result<T> {
data class Success<T>(val value: T): Result<T>()
class Fail<T>: Result<T>()
fun value(onSuccess: (T) -> Unit, onFailed: (Result.Fail<T>) -> Unit) {
return when (this) {
is Result.Success -> onSuccess(this.value)
is Result.Fail -> onFailed(this)
}
}
}이제 합성식에 정수를 문자열로 바꾸는 연산을 추가해 봅시다.
val flow1 = a(10) map ::d flatMap ::a map { "SUCCESS :: $it" }이 값을 출력해 봅시다.
flow1.value(
onSuccess = { println(it) },
onFailed = { println("failed")}
)
//출력
SUCCESS :: 10000아주 쉽게 붙일 수 있습니다. 함수 $f$는 항상 Result.Fail을 반환하도록 작성해 봅시다.
fun <T> f(a: T): Result<T> {
return Result.Fail()
}중간에 $f$를 합성해 보겠습니다.
val flow1 = a(10) map ::d flatMap ::f flatMap ::a map { "SUCCESS :: $it" }
flow1.value(
onSuccess = { println(it) },
onFailed = { println("failed")}
)
//출력
failed원하는 대로 출력되었습니다. 다시 map과 flatMap을 봅시다.
infix fun <T, R> Result<T>.map(functor: (value: T) -> R): Result<R> {
return this.flatMap { value ->
Result.Success(functor(value))
}
}
infix fun <T, R> Result<T>.flatMap(functor: (value: T) -> Result<R>): Result<R> {
return when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
Result.Fail()
}
}
}map은 내부에서 flatMap을 사용합니다. $f$가 Result.Fail을 반환하면 map 내부의 flatMap은 인자로 전달받은 functor에 상관없이 항상 Result.Fail을 반환합니다. flatMap은 Result.Success일 때만 functor를 실행함을 알 수 있습니다. 그래서 map 함수도 Result.Fail을 반환하게 되는 것입니다.
함수 합성을 통해서 데이터가 계속 흐르도록 하였습니다. 이제 2부에서 함수형 프로그래밍으로 작성한 프로그램을 왜 아래처럼 정의할 수 있는지 이해할 수 있을 것입니다.
$$ 클래스 = 데이터 + 로직 $$
$$ 타입 = { 원시타입, 클래스, 함수 } $$
$$ 프로그램 = 타입 + 흐름 $$
3-6. 추상화와 문맥
3부를 마치기 전에 추상화와 문맥에 대해서 잠깐 살펴보려고 합니다. 4부에서는 다양한 모나드를 직접 구현해 보려고 합니다. 모나드는 왜 다양할까요? 그것은 추상화를 통해서 의미나 문맥을 담기 때문입니다. 말은 어렵지만 실제로는 쉽습니다.
우리가 코드를 작성하다 보면 값이 있을 수도 있고 없을 수도 있습니다. 그리고 때로는 비동기 실행도 필요합니다. 어떨 때는 A 또는 B를 선택해야 합니다. 이런 의미를 모나드가 담을 수 있는 것입니다.
$$ f: X \rightarrow Maybe[Y] $$
함수 $f$를 실행하면 Y 타입의 결과값이 있을 수도 있고 없을 수도 있습니다. 방금 우리는 함수 정의에 어떤 의미를 담았습니다!
$$ g: P \rightarrow Future[Q] $$
함수 $g$를 실행하면 Q 타입의 결과값을 지금이 아닌 미래의 어느 시점에 얻을 수 있음을 나타냅니다.
3-7. 정리
지금까지 배운 모나드를 정리하면 아래와 같습니다.
- 구체타입을 추상화한 타입
- 추상화 속엔 사이드이펙트도 포함할 수 있다.
- 사이드이펙트가 있는 함수를 순수함수로 바꾸어 주는 것
- map과 flatMap을 통한 함수 합성으로 데이터가 계속 흐를 수 있게 해 주는 것.
- 따라서 Monad는 Side Effect를 내포하면서 map과 flatmap을 정의한 타입
- 모나드는 문맥을 담는다.
알림 이 글은 데이블 기술블로그에 올린 글을 제 블로그에 다시 올린 글임을 알려드립니다.
피드백 주신 분들
- 문상철님
- 2021년 10월 15일.
정수 집합 Z에 × 연산은 열려 있습니다.가 아닌정수 집합 Z에 × 연산은 닫혀 있습니다.가 옳은 것 같습니다.- 피드백 감사합니다 🙇♂️